The Solar Sprint PV Panel

Basic Electricity Review

To understand Photovoltaics, it is necessary to know something about electricity. There are three very important concepts, Voltage, Current, and Power.

Voltage, measured in Volts, is a measure of the strength of the electricity. It is analogous to pressure of water in a hose.

Current, measured in amps, is a measure of the number of electrons flowing through a wire in a particular time. It is analogous to gallons of water per second flowing in a hose.

Note that voltage and current are totally different concepts. If the nozzle on the hose is closed, the flow (current) is shut off, but the pressure (voltage) is high. If the nozzle is opened, flow (current) is high, but pressure (voltage) drops. If the nozzle is partially open, there is both flow and pressure.

Just as flow of water through a hose causes pressure drop due to friction, current flow in a wire causes voltage drop.

The third concept is that of power. Power is simply voltage times current. It is also the amount of energy that is delivered in a unit of time.

An important difference between water flow in a pipe and electricity is that electric current always travels in a closed loop, a "circuit".

The Photovoltaic Panel

The first major component in a Solar Sprint car is the Solar or Photovoltaic (PV) panel. This is its power source. The more power that can be delivered to the motor, the better the car will accelerate.

The P-N Junction

Photovoltaic panels convert sunlight into electricity. The Solar Sprint solar panels are composed of 6 silicon cells connected in series. The most important feature of the solar cell is its layered structure. The bulk of the cell is made of "P-type" silicon. P-type silicon is mostly pure silicon that contains a small amount of impurity (or dopant), typically Boron, which gives the material a special electrical characteristic, a deficit of electrons (also known as a surplus of "holes").

On top of the P-type substrate is a layer of "N-type" silicon. This layer is nearly pure silicon, but containing a small amount of a different dopant (typically Phosphorous). The characteristic of this layer is that it has a surplus of electrons.

The interface between these layers is known as a P-N junction, and this is the central feature of the solar cell. It has very special electrical properties. P-N junctions have the characteristic that they behave like a one-way door for electricity (with a spring on the door). Because of this characteristic they are used in all types of electronic equipment.

If voltage is applied across the P-N junction with the positive connected to the P side, a small residual potential must be overcome (typically less than a volt), then the current through the junction increases rapidly. The junction is "forward biased".

If voltage is applied in the reverse direction across the P-N junction, current flow is blocked. The junction is "reverse biased".

One can plot a graph of current voltage for a diode, and it will look something like the following:

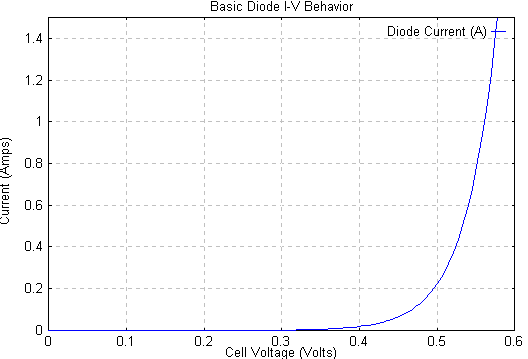
This is known as the "I-V" characteristic of the device.

Light

When photons of light pass into silicon, they have some probability of being absorbed. When they are absorbed, the effect is to knock an electron into a higher energy state. This free electron is likely to roam around the silicon's crystallne structure for a while. It also creates a "hole", and in fact the hole can roam around the silicon, too. If the photon is absorbed far away from the P-N junction, the hole and electron simply recombine and produce heat. If it occurs near the junction, the effect is that additional current is injected into the junction. The amount of current is directly proportional to the amount of light that falls on the cell. The extra current through the junction causes the voltage across it to increase.

Take the I-V characteristic of the P-N junction, shift it downward by an amount corresponding to the light-injected current, and flip it, and the result is the following I-V curve that is often presented for PV cells:

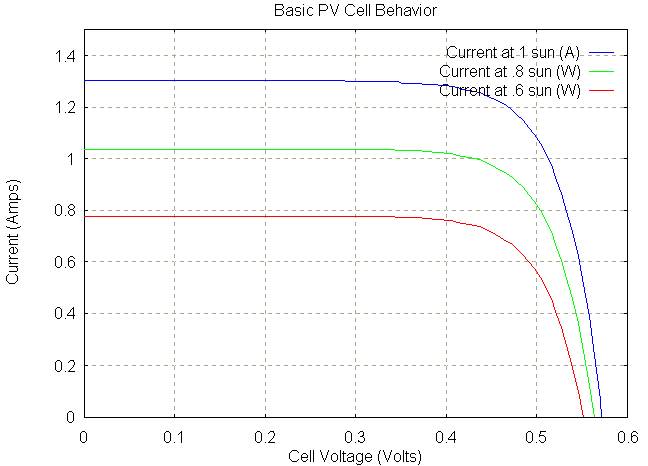
This graph represents the behavior of a solar cell at particular intensities of solar radiation.

These are very important curves. Note the point at which a curve intersects the vertical axis. This is known as the short circuit condition, and it defines how the cell operates if a wire is connected between its terminals, shorting it out. The current flow here is known as Isc. Because there is no voltage, the cell delivers no power.

Now note the point at which a curve intersects the horizontal axis. This is where the cell operates if it is unconnected. This is known as the open circuit condition, and the voltage produced is denoted Voc. Because the current is zero, no power is delivered.

For each point on the graph, the voltage and current can be multiplied to calculate power. If this power output curve is plotted on the original graph for full sunlight, we get the following graphs:

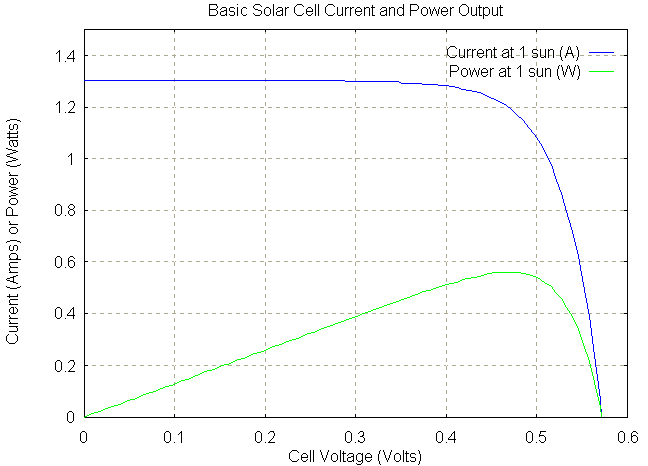
Note that the power is maximum at a single operating point. This is known as the "Maximum Power Point", or MPP. If one is to get the most out of their solar cells, it is essential to operate around the MPP. The quality of a PV cell is often rated with a characteristic called its "Fill Factor". This is defined as the maximum power produced (at MPP) divided by the product of Isc and Voc. One can see that the Fill Factor will always be less than 1.

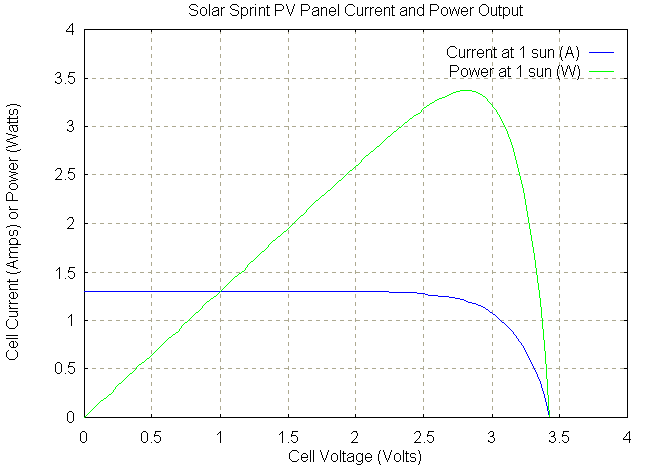
As mentioned, the Solar Sprint PV panel is actually 6 cells connected in series. The following graph shows an approximation of the I-V and power output curves for these panels:

Sun Angle

It has been seen that the PV panel's output current is proportional to the solar radiation that strikes it. It is important to understand that this radiation level is reduced if the panel is not pointing directly at the sun. Like other parts of this problem, the amount that it is reduced can be calculated. The cell’s output must be multiplied by the cosine of the angle of incidence of the incoming light. When designing a Solar Sprint car, a possible design feature would be the ability to adjust the angle of the PV cell.

The following figure shows how the angle of incidence affects PV cell output.

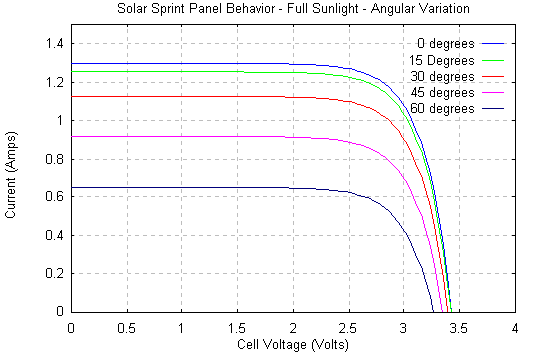
Note that small variations in angle do not reduce output very much. Even a 60 degree angle of incidence only makes the output decline by one half.

The Electrical Model of the PV Cell

We can define an electrical circuit that acts just like our ideal solar cell, and draw its schematic diagram (which we will use later). It is simply a current source in parallel with a diode (our P-N junction). A current source is a device that produces a constant current. In this case, the current is proportional to the intensity of light that falls on the cell.

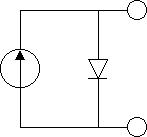
The diode has the I-V characteristic that we graphed above. If we do not connect the cell to anything, current from the current source just circulates back around through the diode. A voltage is created across the diode. This is the open circuit condition. If we short the cell, all of the current is diverted away from the diode and flows through the short. Voltage output is zero. This is the short circuit condition.

Real solar cells have characteristics that degrade their performance compared to the ideal. In particular, their wiring has some resistance to the flow of current. This is represented electrically by a resistor in series. Likewise, there is some resistance that is in parallel with the current source and diode that drains some amount of power from the cell. To be more complete, then, the equivalent circuit looks like the following.

The actual Solar Sprint PV panel consists of 6 PV cells connected in series. The Isc of this panel in full sunlight is about 1.3 amps. Its Voc is about 3.4 volts.

Measurements of the Solar Sprint Panel

Measuring the basic parameters of a PV panel is fairly easy. All you need is the panel, a Volt Ohmmeter (with a DC Amps scale), a couple of resistors, and a sunny day. Here is how I measured a Solar Sprint panel.

Pointing the panel at the sun, I measured the voltage that the panel produced. The panel that I tested produced about 3.3 volts. When the meter is measuring voltage, there is almost no current flow. So, this measurement was the Voc of the panel. Then I set the meter to measure DC Amperes, and connected it across the panel’s terminals. It registered 1.35 Amperes. Because the meter has very low resistance when measuring current, this represents the Isc of the panel. Then I measured the panel’s voltage with a couple of different resistors connected across the leads. With a 2.5 ohm resistor, it produced about 2.9 volts. I calculated that the current was 1.16 amps (I = V/R by Ohm’s law). Actually, by measuring the cell with a variety of resistive loads, I was able to plot points on the I/V curve, and determine that the maximum power point occurred with a load of about 2.5 ohms (remember, power is V*I, or V**2/R).

To produce the graphs that are shown above, I fiddled with the coefficients of the basic PV equations to get a curve that reasonably matched the data that I had measured from the panel.

To contact me...

Return to Chuck Wright's home page http://www.chuck-wright.com