Combining the Motor with the PV Panel

The Permanent Magnet Motor

A motor converts electricity into mechanical energy. The Solar Sprint motor is what is known as a Permanent Magnet Direct Current (PMDC) Motor. The operation of PMDC motors is well understood, and given a few basic parameters about a particular motor, it is possible to predict it's operational characteristics quite accurately. The motors supplied with the Solar Sprint kits are not of high quality, having high mechanical friction as well as low quality brushes and bearings that probably won't last a long time. Also, no performance data is available for them. The first problem can be solved only by buying a better motor. However, performance data can be obtained from some fairly simple measurements.

The Ideal Motor

Electrically, the ideal motor looks like a resistor in series with a voltage source. The resistor represents the resistance of the motor windings. PMDC motors act as generators whenever thy are turning, whether they are turning themselves or are being turned. They produce a voltage that is proportional to their speed. The voltage source represents this generated voltage, which is in proportion to the motor speed, and bucks the flow of current in the motor. The generator voltage is equal to the generator constant, Kg (in volts per RPM), times the speed of the motor. The generator voltage inside a motor is also called "back EMF".

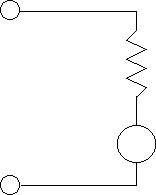
When current flows through the PMDC motor, torque is produced at the motor shaft. This torque is equal to the torque constant, Kt (in N-m/A), times the motor current. With increasing speed, the back EMF causes reduced current flow (and hence reduced torque).

A little appreciated fact is that the generator constant Kg and the torque constant Kt are actually the same. Although often expressed in different units and specified separately, if converted to compatible units, they will be seen to be the same. So, if one can measure one, a simple unit conversion will yield the other.

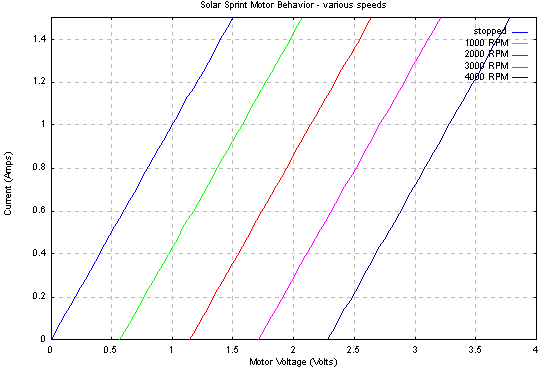
An equivalent circuit for the motor was shown above. Just as we drew an I-V curve for the PV panel, we can draw one for the motor. This will be of interest when we connect the motor to the PV panel. The motor will have a unique curve for each operating speed. Several of these are displayed in the following graph:

Power Losses

In an ideal motor, all applied power would be delivered to the load. In a real motor, there are several places that power gets lost.

One major loss is in the electrical resistance of the motor windings. It can be calculated as I**2 R. Because motor current is proportional to the torque generated by the motor, resistive losses are also proportional to motor torque.

The second major loss is friction. As with the loss in the winding resistance, friction converts applied energy into heat. Friction can be considered to be composed of several components. "Standing friction" must be overcome before the motor will start. "Running friction" is ordinarily less, and is seen as a torque resisting motor turning. It is the same at all motor speeds.

We will ignore starting friction, as we ordinarily apply enough voltage to get over it very quickly.

Because torque is related to the motor curent by the torque constant, frictional torque will show up as a constant running current for the unloaded motor.

There are other possible opportunities for losing power in the motor. In an iron core motor, changing magnetic fields actually induce current flow in the iron core (eddy currents). These currents result in a power loss that increases with motor speed.

Another loss stems from the fact that the winding has inductance. When current flows through a winding, energy is stored in the magnetic field. When current is stopped by commutation, this energy must go somewhere, and it doesn't go anywhere that is useable! (this is the source of brush sparking, for example). This energy loss increases with increasing motor speed.

There are also frictional forces due to aerodynamic effects. These losses increase with increasing motor speed.

Efficiency

We are interested in delivering the maximum amount of power to the load, and want to minimize power dissipated as heat. We can express the efficiency of a motor as the power delivered divided by the power input. If we are able to measure the torque delivered and operating speed of a motor, we can calculate its output power as simply T * S. The input power is just the appled voltage times the current.

There is an easier way of estimating motor efficiency than by actually measuring output torque and speed. This can be done by considering the electrical power that is not lost to friction or winding resistance. Considering the equivalent circuit shown above, we are interested in the portion of the current that corresponds to the delivered torque, and the portion of the voltage that is not dropped across the motor resistance.

Measuring the running but unloaded motor will reveal that it draws a current that is relatively independent of speed (the small speed-dependent portion corresponds to the other losses mentioned above, and will be ignored here). This current, If, corresponds to the frictional loss of the motor. We can thus consider that the current that is actually being used to turn the load is simply

The voltage that is actually applied to turn the load is simply

Hence, the efficiency of the motor can be calculated as

Efficiency of a motor is the power delivered (its torque times its speed) divided by the power input (voltage times current). The following graph shows efficiency as a function of torque for the Solar Sprint motor, and also for a motor of similar design, but with much lower friction.

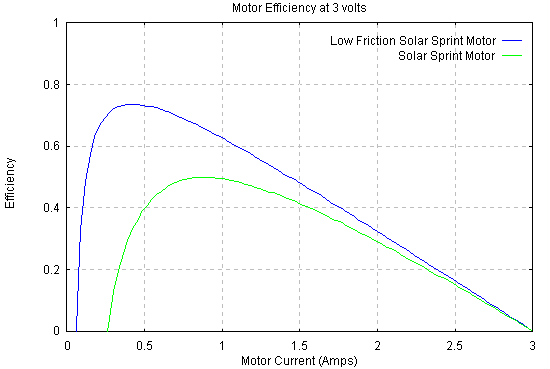
The graph indicates that this motor has a maximum efficiency of less than 50 percent. The curve for the low friction case shows a much higher efficiency, indicating that the motor's friction is a significant problem.

The horizontal axis of this graph is current. Note that this current is related to torque (delivered plus frictional) by the torque constant, so this is also a graph of efficiency versus torque.

Another thing to remember is that, for a particular applied voltage, speed and torque are intimately related. Writing the voltage equation for the motor, we get

Rearranging:

Knowing that torque is KI:

So the speed of the motor is maximum when torque is equal to the frictional torque. This is the "no load speed". Speed declines linearly with increasing torque increase until it reaches the stall condition.

Measuring Motor Characteristics

The easiest parameter of the Solar Sprint motor to measure is it's electrical resistance. This can be measured with an ohmmeter. Because this motor has rather poor brushes, it is a bit difficult to get a consistent reading. It helps to run the motor for a while first. On the samples that we tested, a motor resistance of about one ohm was measured.

Secondly, we wish to know what the generator constant (or the torque constant) is. This is a little harder. There are different ways of approaching this. The way that we chose was to drive the motor at various speeds and measure the voltage that was generated at its terminals. We happened to have a second DC motor with a built-in tachometer, which produced a frequency proportional to its speed. Driving our Solar Sprint motor at various speeds and recording the generated voltage, we determined a motor constant of 0.0054 volt-sec (or about 0.57 volts/1000RPM). So, we know that the torque constant is 0.0054 nt-m/amp.

The third important constant to measure is the frictional torque. We can measure the motor current (when running), and as expected, see a reasonably constant current draw. On our sample of SOlar Sprint motor, it was about 0.26 amps. Multiplying by the torque constant, we conclude that frictional torque is 0.0014 nt-m.

The Combination

Because the motor is connected directly to the PV panel, we know that the motor will operate at a current and a voltage that is on both the I-V curve for the PV cell and the I-V curve of the motor. It is where these two functions intersect.

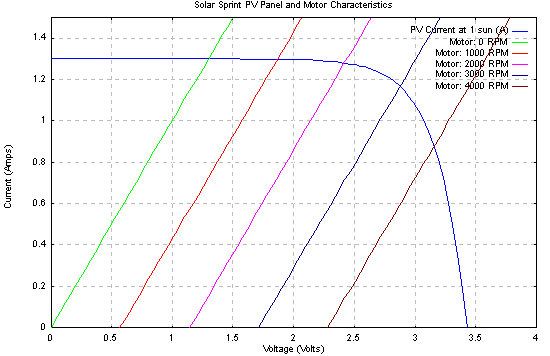
Upon starting, the system operates at the intersection of the leftmost motor curve and the PV curve. As motor speed increases, the operating point slides to the right along the PV curve.

We might wish to know how this is relevant to the performance of the PV car. Since the main object of this car is high acceleration, we should direct our exploration to power delivery. At any given time, delivering more power will produce better acceleration. We have already seen that the PV panel has a single optimal operating point. We should now explore the optimum operating point of the motor/panel combination.

Knowing the basic parameters of the motor, we can calculate its efficiency at any operating point. Knowing that the motor/PV panel combination has a particular set of operating points, we can calculate the efficiency of the combination at these points. The following graph shows this.

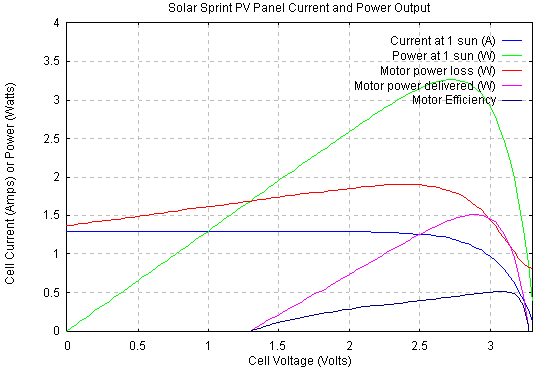
This mechanical power goes partially to motor friction (which in the Solar Sprint motor appears to be large), car friction, and to accelerating the car.

Notice a few things. The motor power curve has a peak. This peak is less than that of the PV panel, so we can see that much of our PV power will be wasted. The peak does not coincide to the PV panel’s MPP. Because the power delivery peak is narrow, our car is likely to spend much of its time operating at other than the maximum power delivery point.

In the simplest car design, there will be few options in the basic design. The motor is chosen, as is the PV panel. The motor will be connected directly to the PV panel. The main design option will be choice of the gearing ratio. How do we select the best gear ratio? Should we consider other, more advanced techniques to improve the car’s performance?

To better understand the possibilities, we can turn to more advanced tools. When confronted with complex analysis tasks, most modern engineers rely on numerical simulation on digital computers. The next part of this article shows how such an electronic circuit simulator can be used to predict the operation of a Solar Sprint car, and to explore design tradeoffs.

To contact me...
Return to Chuck Wright's home page http://www.chuck-wright.com